|
|
 ギターの力学 総まとめ編 その2 ギターの力学 総まとめ編 その2ここでは、フレットを押さえた時に、どれ位音程が狂うか・・・を考えます |
![]()
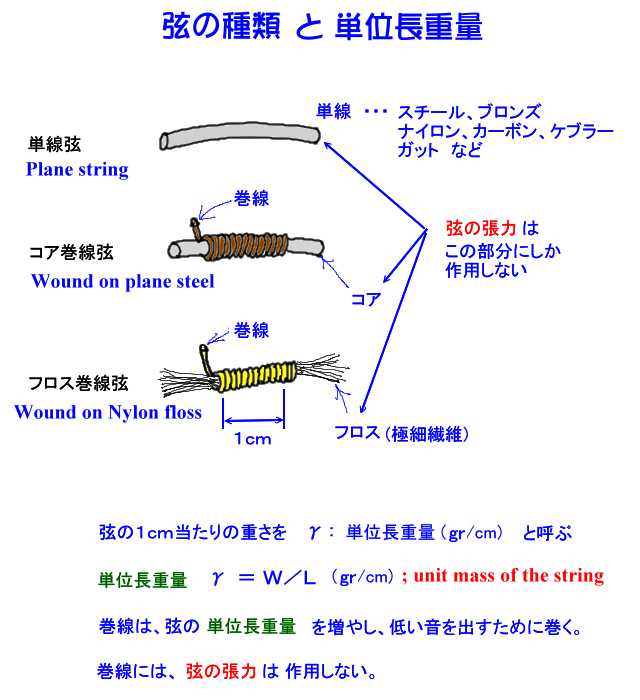
アコースティックギター弦には、下の図のように色々な構造のものが使われています。
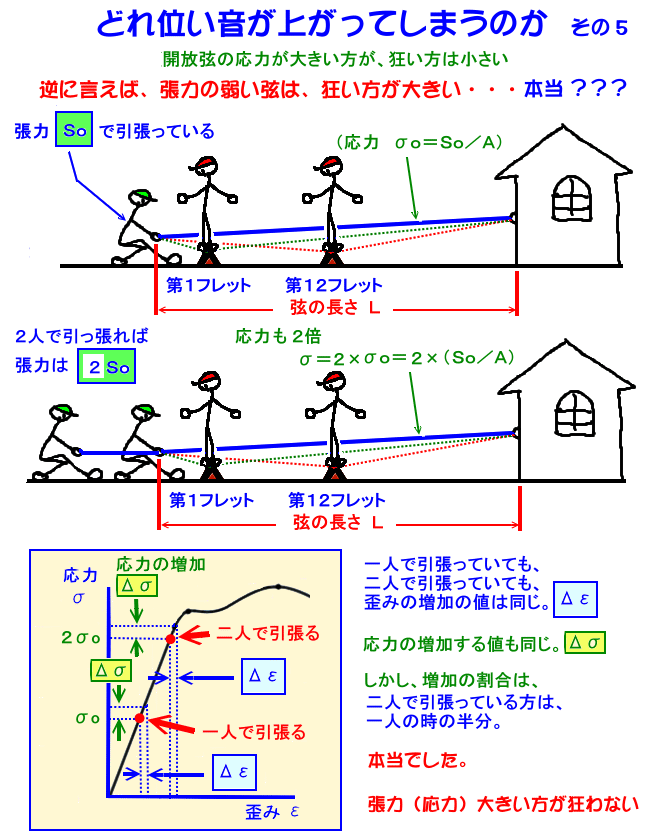
弦の張力がほぼ同じであっても、音程の狂う程度は弦の構造によって大きな違いが有ります。そこで、それらを正しく掴むために、応力と歪み・・・と言う考え方を使います。 これは、材料力学と言う分野になりますが、工学系の方で有れば、すごく簡単な話です。
低音を演奏するエレキベースでは、弦の単位長重量を増やすために、2重、3重に巻線の巻かれた弦が使用されています。
左から 4弦エレキベース用、Medium String の #1, #2, #3, #4
![]()
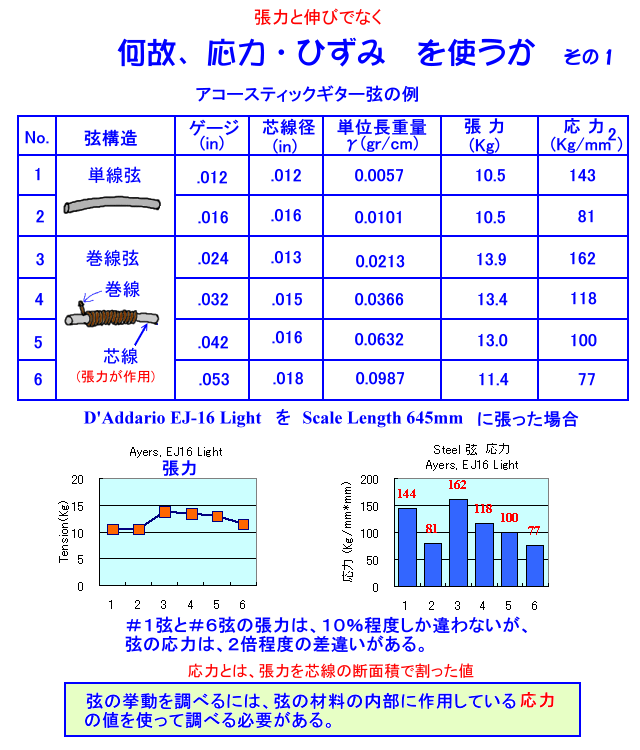
何故、応力・歪み を使うか
この図は、弦の張力が同じ程度であっても、弦の内部の芯線部に働いている力・・・ 応力 には、大きな違いがある・・・と言うことを示しています。
![]()
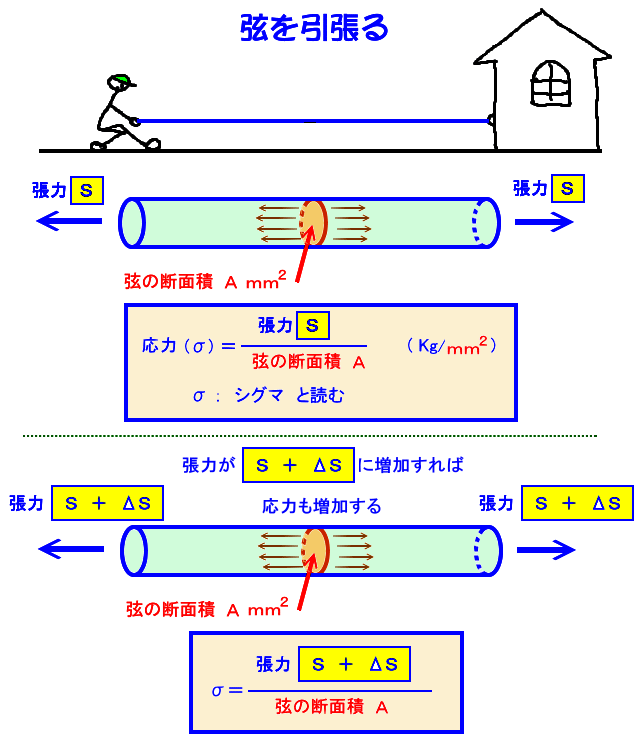
応力とは、何でしょうか
弦を引張ったとき、引張る力・・・張力 を、弦の断面積で割った値を 応力 と言います。
![]()
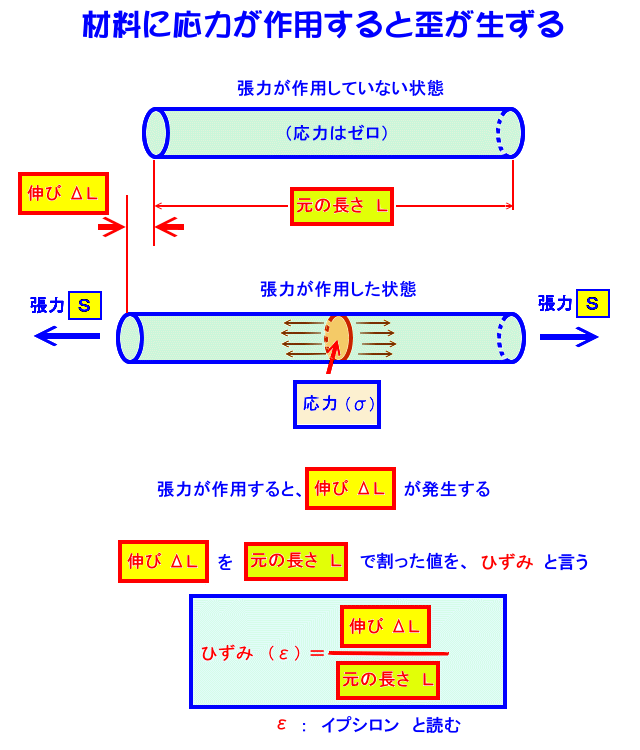
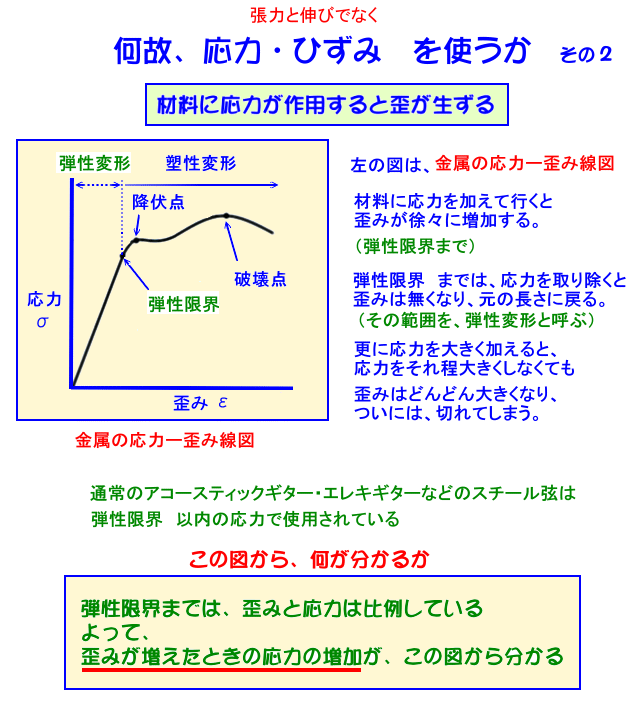
材料に応力が作用すると歪みが発生します
歪み・・・と言う値は、伸びた量を元の長さで割った値ですので、仮に、短い弦が少し伸びた・・・と言うのと、長い弦が沢山伸びた・・・と言う場合、歪み の大きさは同じ程度になります。すなわち、引張っている力である張力や伸びた長さではなく、応力と歪み・・・と言う値で物を見ると、材料の変形した程度と、内部に働いている力の程度を知ることが出来るのです。
![]()
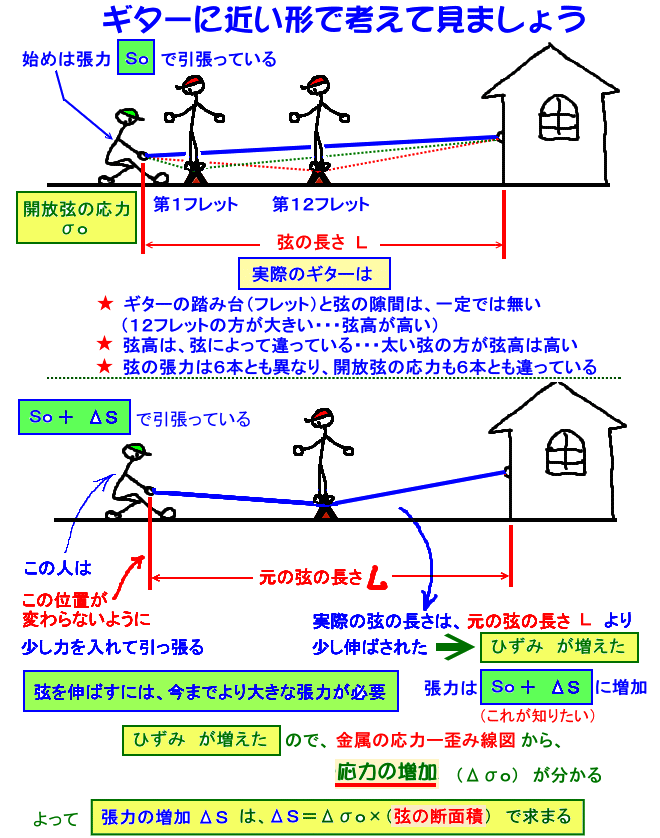
材料に応力が作用すると歪みが発生します
金属製のスチール弦でも、ナイロン弦でも、材料に力が加わり、応力 が作用すると、その材料には必ず 歪み が生じます。
逆に考えれば、歪み が生じている材料には、その程度に関係して 応力 が作用している・・・と言うことです。
それを示したものが、下記の図です。
上の図は、金属製のスチール弦を引張った場合の、応力と歪み の関係を図示した物です。何故、こんなややこしい話が、ギターの話の中に出てくるのか・・・と、疑問を持たれる方は多いと思いますが、もう少し辛抱して先に進んでください。
きっとお役に立ちます。
![]()
ギター弦の応力・歪み の関係は、こうなっています
上の図は、歪みの増えた値 が分かれば、弦の張力がどれ位増加するか、すなわち、張力の増加 が分かる・・・と言うことを示しています。張力の増加 を知りたい訳・・・それは、張力が増加 すれば、音が高くなってしまうからです。
音が高くなってしまう程度・・・を知るために、張力の増加 を知る必要があるのです。
![]()
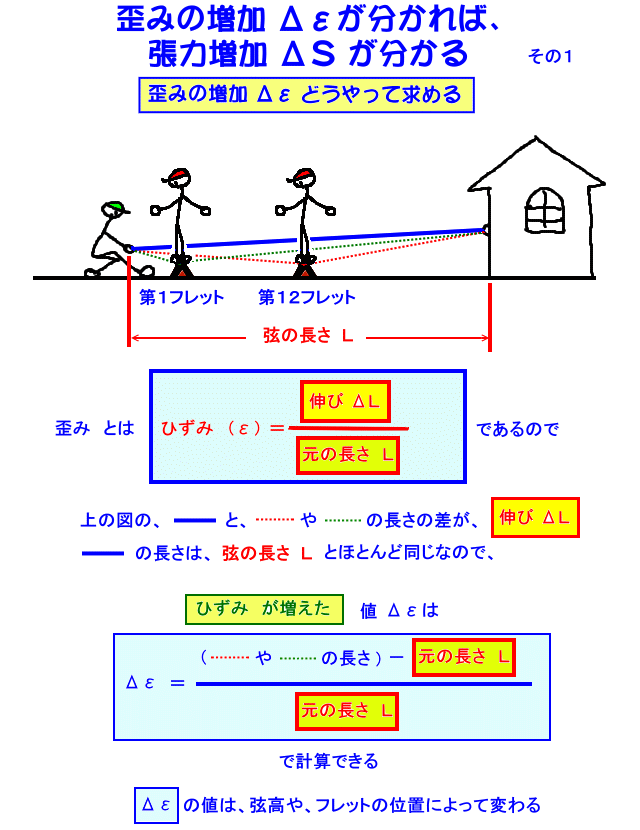
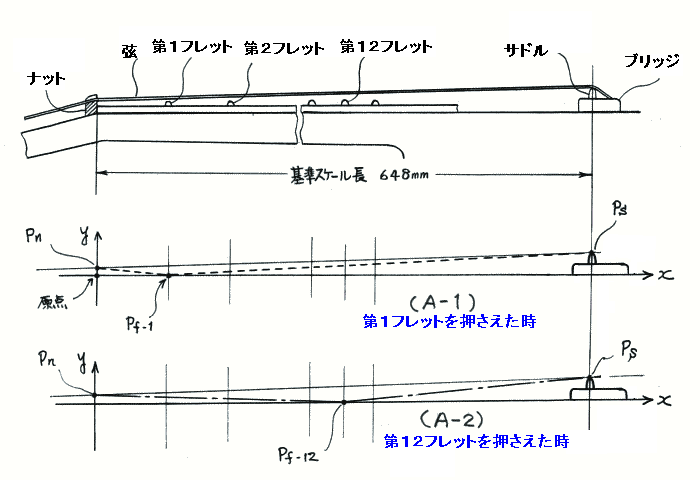
ギター弦の歪み とは、このように考えます
ギター弦の歪み とは、フレットを押さえた時の弦の長さと、元の開放弦の長さから、上記のように計算できます。ここで大切なことは、ギター弦の歪み は、上の図の 踏み台の高さ・・・すなわち、弦高 や、フレットのポジション に依って変わる・・・と言うことです。
実際の ギター弦の歪みの計算は、ピタゴラスの定理 などの簡単な計算で求めることが出来ますので、ここでは省略致します。
![]()
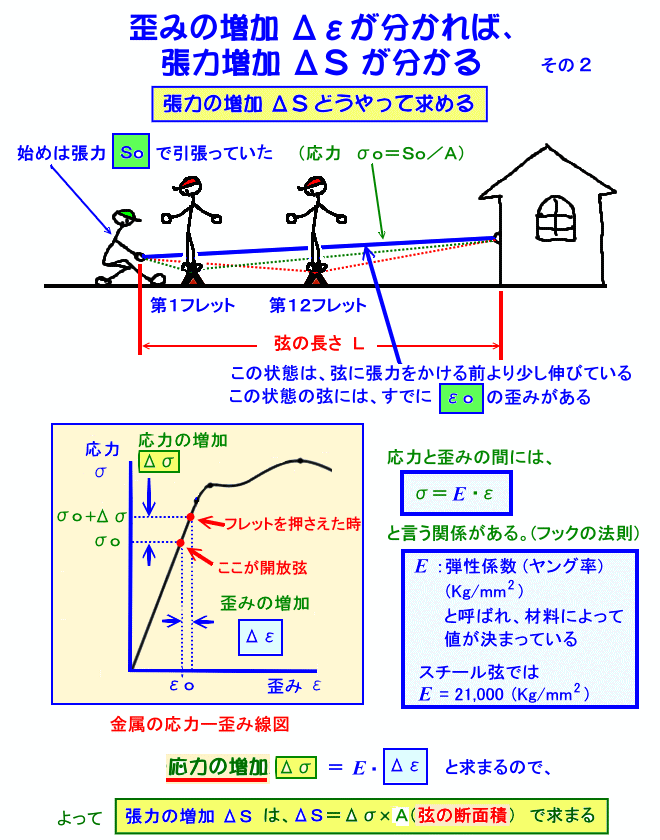
歪みが分かれば、応力が分かるので、音程の狂いを発生させる 張力の増加 が分かる
一般的に、材料力学 と言う分野で使われる、「応力−ひずみ線図」 に於いて、鋼硬線 すなわち、ピアノ線 (Steel String) のような、硬く、伸びに強い材料の場合、E 縦弾性係数(ヤング率)=21,000 (Kg/mm*mm) と言う数値が使われます。
この値を用いることによって、フレットを押さえた時の 歪みの増加 の値から、弦の張力の増加量 を求めることが可能になりました。
![]()
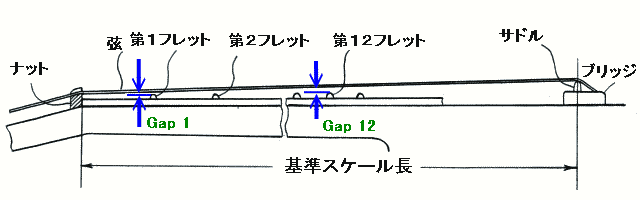
弦をフレットに押さえた時、弦の歪みの増加量・・・を計算で求めてみましょう
弦をフレットに押さえるのですから、弦高を予めキチット決めておく必要があります。
通常は、第1フレット部での弦の高さ Gap 1 は、ナットの溝の深さで調節し、第12フレット部での弦の高さ Gap 12 は、サドルの高さで調節します。
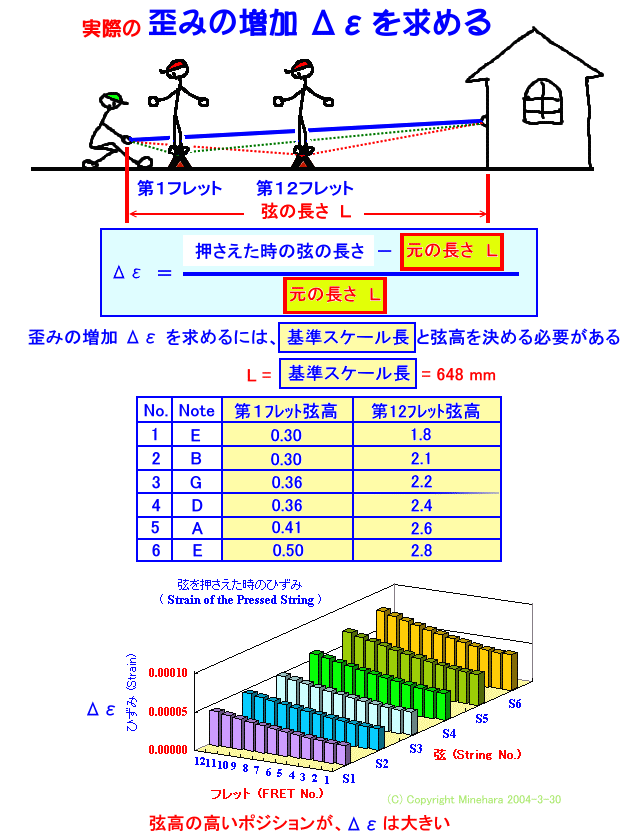
ここでは、弦高 が次の表の値に調節されたギターとします。
#
Note
第1フレット部での弦の高さ Gap 1 (mm)
第12フレット部での弦の高さ Gap 12 (mm)
1
E
0.30
1.8
2
B
0.30
2.1
3
G
0.36
2.2
4
D
0.36
2.4
5
A
0.41
2.6
6
E
0.50
2.8
この値は、指板やフレットが相当良く作られたギターでないと設定できない値で、この調整値であれば、大変弾き易いギターであることは間違い有りません。
それでは、弦の伸び ΔL を計算してみます。
フレットを押さえた時の、弦の伸び ΔL の計算には、多少、近似 的な計算を用います。 計算方法の詳細は省略し、ここでは、その結果のみ示します。
基準スケール長 648mm の各フレットを押さえた時の、弦長合計 (mm)
Fret #
基準スケール長 648mm 、
ナットからフレット位置までの寸法 (mm)第1弦
E第2弦
B第3弦
G第4弦
D第5弦
A第6弦
E0
0
648.000
648.000
648.000
648.000
648.000
648.000
1
36.368
648.016
648.018
648.019
648.023
648.026
648.030
2
70.697
648.017
648.018
648.020
648.023
648.026
648.030
3
103.100
648.017
648.019
648.020
648.024
648.027
648.031
4
133.682
648.018
648.020
648.021
648.025
648.029
648.033
5
162.549
648.019
648.021
648.023
648.027
648.030
648.034
6
189.794
648.020
648.022
648.024
648.028
648.032
648.036
7
215.513
648.022
648.025
648.025
648.030
648.034
648.038
8
239.785
648.023
648.026
648.027
648.031
648.036
648.040
9
262.696
648.024
648.020
648.028
648.033
648.038
648.043
10
284.323
648.026
648.028
648.030
648.035
648.040
648.045
11
304.734
648.027
648.030
648.032
648.037
648.043
648.048
12
324.000
648.029
648.031
648.033
648.039
648.045
648.051
この数値を良く見て下さい。 開放弦の長さ L は、648.000 mm でしたが、第6弦の第1フレットを押さえた時 、弦長合計 は、 648.030 mm となりました。
この僅かな差、 0.030 mm が、弦の伸び ΔL で、弦の張力変化を起こすのです。
上の表の数値を良く見て下さい。 同じ弦 であれば、弦長合計 は、 第12フレットを押さえた時 、が一番大きくなり、
同じフレット であれば、下の弦になるほど、弦長合計 は、 大きくなっている事が分かりました。
弦をフレットに押さえた時、弦がどれくらい伸びるか・・・が分かりましたので、
L の長さの弦が、ΔL だけ伸ばされたのですから、ひずみ Δε は Δε=ΔL/L で計算できます。
これは、弦高によって決まってきます。
ひずみ Δε の値は、この図のように計算されました。 その値は、0.0000** と、大変小さな値ですが、こんな小さな値が、音程の狂い に大きく影響しているのです。ここで大切なことは、ひずみ Δε の値は、弦高 に依って決まりますので、弦高 の高いギターは、フレットを押さえた時の音程の狂い も大きい・・・と言うことになります。
しかし、 ミネハラ スーパーチューンシステム TM なら、貴方の好みの弦高 の値に従って、音程の狂い を完璧になくすセットアップが可能となります。
もう少し先までお読み下さい。
![]()
歪みの増加量から、音程の狂い を求める方法を説明します
始めに、考え方を復習しておきます。
音程の狂い は、下記の手順で求めのこととしましょう。
![]()
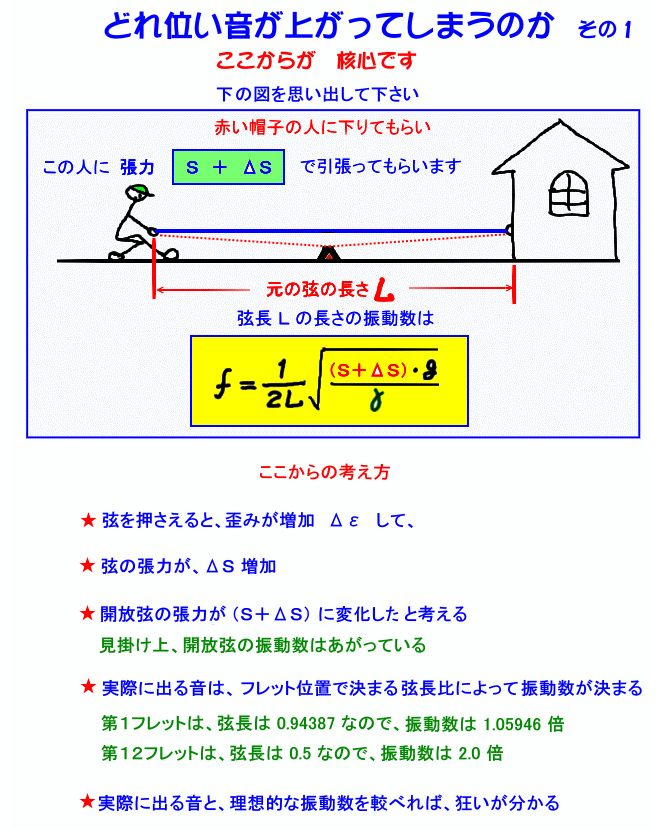
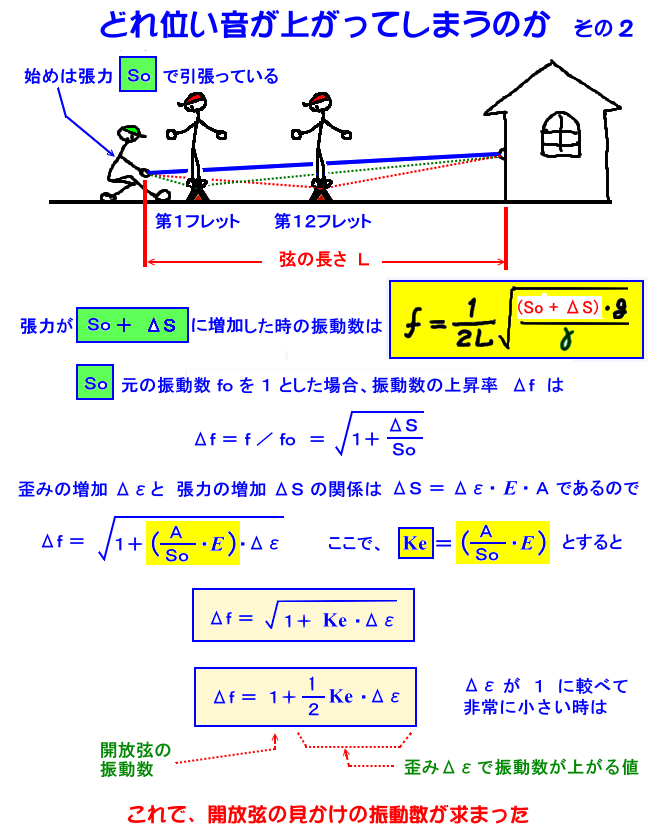
張力増加によって、開放弦の見かけの振動数がどれ位上がってしまうか・・・を求めます
ここで、 Ke ひずみ当たりの振動数上昇係数 (弦係数) と言う新しい数値を定義しました。
ミネハラ スーパーチューンシステム TM の特徴は、ギターの6本ある弦に関して、その弦の音程の狂い易さ・・・を示す、Ke (工房ミネハラ では 弦係数 と名付けました) と言う値を導入したことにあります。 すなわち、6本の弦とも、音程の狂い方は皆違っている・・・と言うことです。
と言うことは、ギターの6本の弦に対しては、一本一本、それぞれに最適な解決方法をとる必要がある・・・と言うことになります。
ギター弦のパッケージには、ゲージ(太さ) は必ず表示されています。 中には、テンション(張力) も表示されているものもありますが、本当に必要なものは、その弦の音程の狂い易さ・・・を示す、Ke (弦係数) の値です。 将来はKe (弦係数)の値もギター弦のパッケージに表示されるようになると便利になると考えております。 Patented (特許第4383272)
![]()
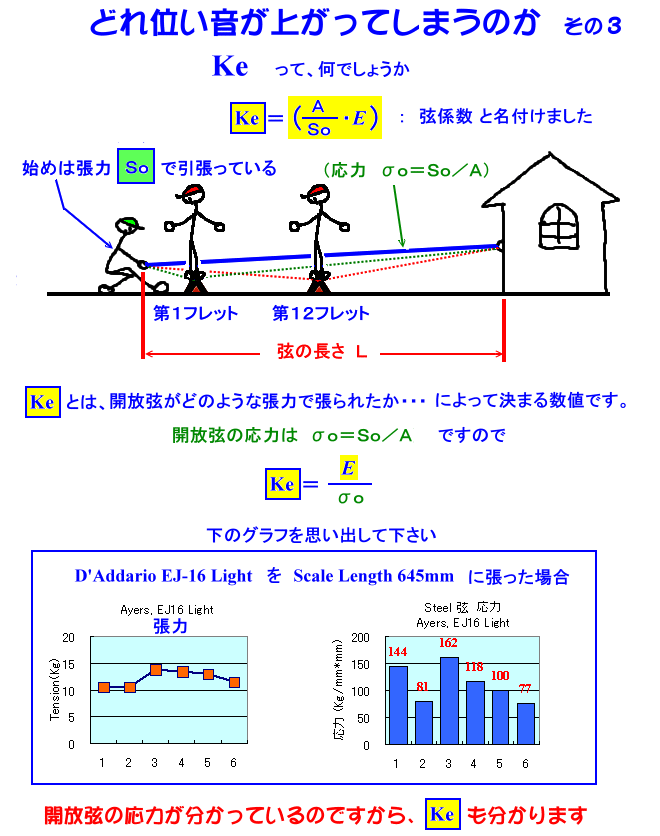
Ke とは、何でしょうか
Ke の値を計算で求めると、下図のようになります。
Ke の値とは、開放弦がどのような応力で張られているか・・・その値によって、フレットを押さえた時に、どの程度 音程が狂い易いか・・・を示す数値と言うことになります。
事例でご説明します。
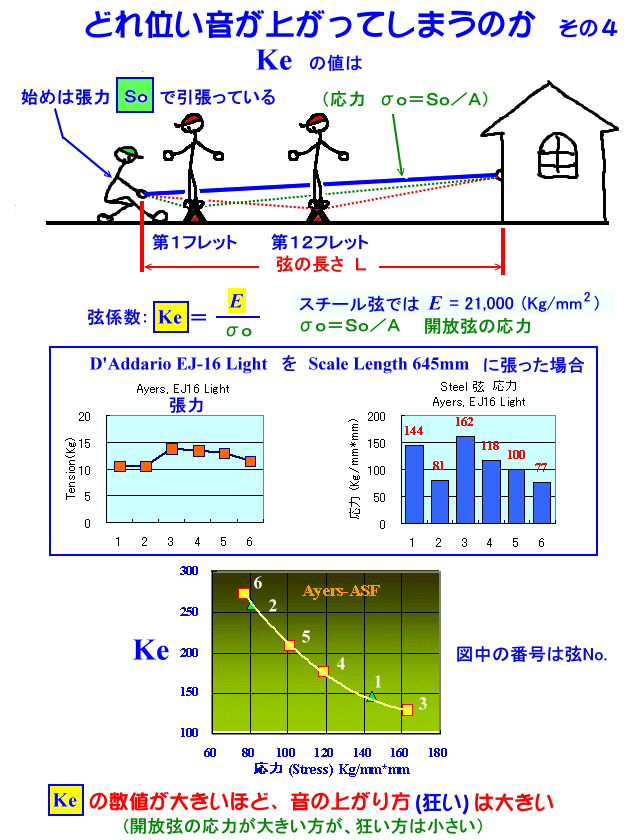
上の Ke の値で示したように、スチール弦のアコースティックギターの場合、開放弦の応力の小さい第2弦の方が、第1弦より音程が狂い易い・・・
開放弦の応力の小さい第6弦の方が、第3弦より音程が狂い易い・・・と言うことは実感されていると思います。別な事例としては、アコースティックギターより、弦の張力の弱いエレキギターの方が、音程が狂い易い・・・と言うことも、実感されていると思います。
エレキギターの第3弦、第6弦は特に音程が狂い易い・・・
Ke の値が大きいほど、音程は狂い易い・・・のです。
![]()
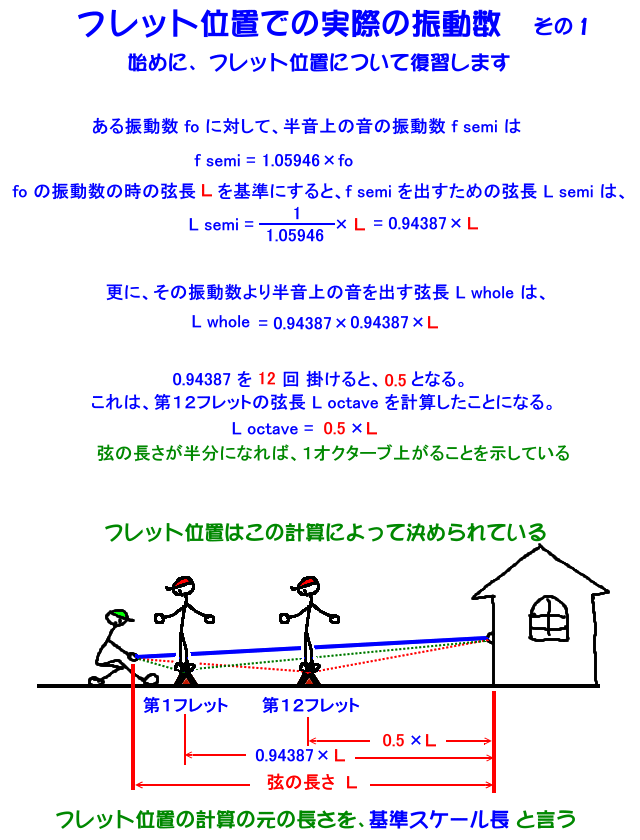
フレット位置での、実際の音程が狂い を求めましょう。
下の図は、フレット位置の復習です。
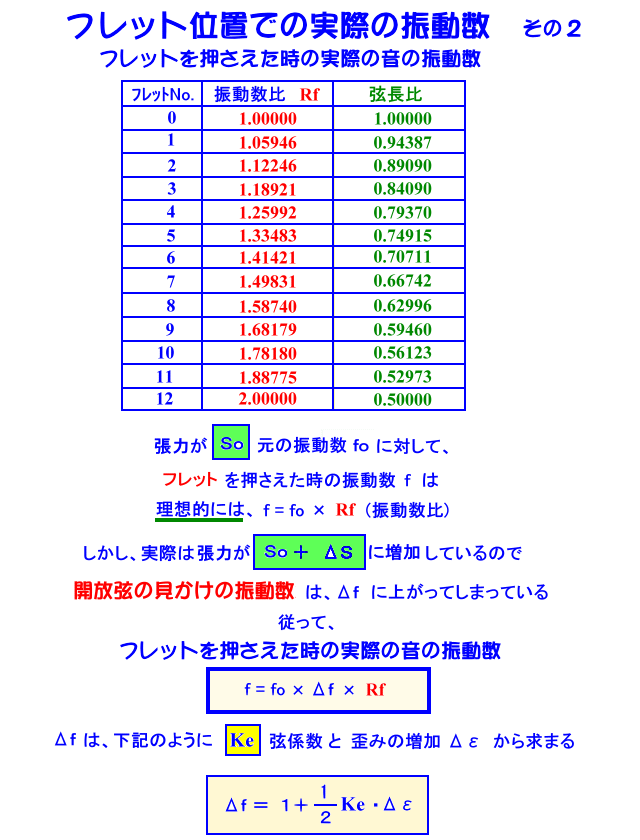
Ke と言う数値を用いて、フレットを押さえた時に開放弦の見かけの振動数が、どれ位上がってしまうか・・・を、Δf として求めることが出来ましたので、
その値に、Rf (振動数比) を掛けた値が、実際の音程の狂い として求まります。
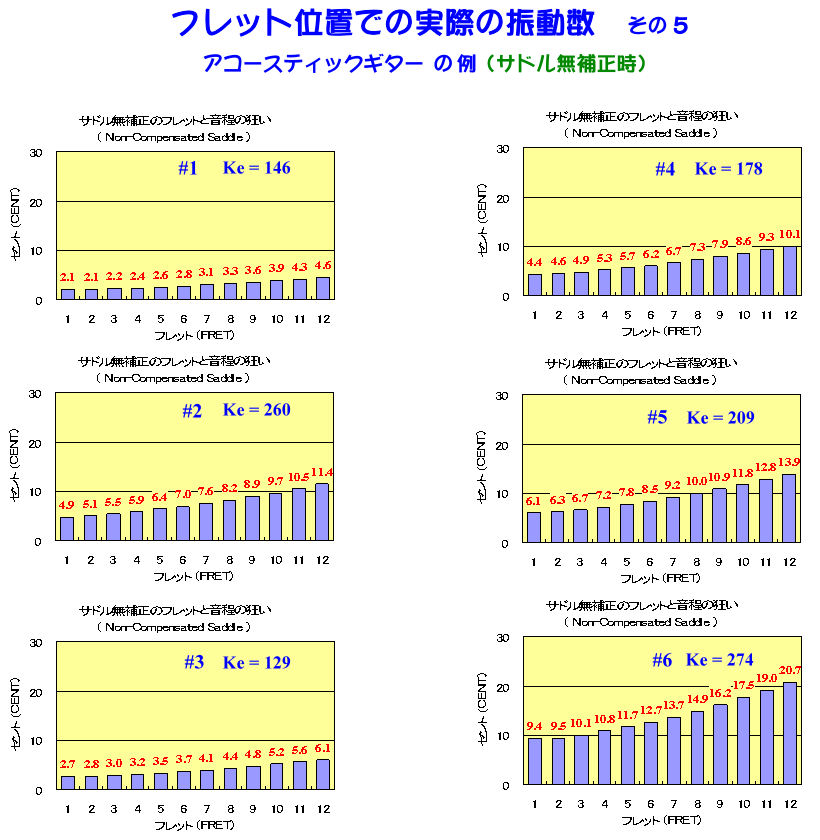
サドルも、ナットも、何も補正しない状態では、こんなに音程が狂っている・・・と言う事が分かりました。
グラフの横軸は、フレットポジション、縦軸は、音程の狂い を示す セント 単位です。
ポイント
フレットを押さえた場合の音程の狂いは、
(1)弦高によって決まる、弦の Δε (ひずみ) の値と
(2)弦の太さ、すなわち、弦のゲージと張力 からきまる、弦係数 Ke
の、2つの要因によってきまる。
計算結果から分かったもの
(1) フレットを押さえると、どのポジションでも、音程は上がってしまう・・・
(2) どの弦も、第12フレット側が 音程が上がってしまう・・・
(3) 音程が上がってしまう程度は、弦のゲージに大きく影響をうける・・・
第6弦 の 第12フレット では、20.7 セント も狂っていることが分かりました。
半音は、100 セント ですので、半音の1/5以上も、音程が上がってしまうのです。 これでは、楽器として成り立ちません。
この値は、理想的に切られた、正確なフレットに対しての計算値ですので、実際はもっと大きな狂いが発生する場合も考えられます。
ポイント
フレットを押さえる・・・と言うことは、どのポジションでも、音のピッチ イントネーションを狂わす最大の要因。
でも、ギターはフレットを押さえて演奏する フレット楽器 なので、しょうがない。
フレットを押さえた時の音程の狂 いを、Ke と言う値 ひずみ当たりの振動数上昇係数 (弦係数) を用いて、定量的に把握する手法を、工房ミネハラ は確立しました。
これにより、「それでは、音程の狂いを低減するには、どうすれば良いか・・・」と言うことも、定量的に把握することができるようになり、
その結果、
Minehara Super Tune System TM
Patented (特許第4383272)が生まれました。
じゃー、実際のギターでは、どうしたら良いのでしょうか ???・・・
更に続きがあります。 ここからが ミネハラ スーパーチューンシステム TM の本題に迫ります。
弦楽器の力学 のページで掲載しているデータの無断転載 ・公開等はお断りします。
工房ミネハラ
Mineo Harada2020/5/10
Updated:2010/12/8
First Updated:2004/3/16