ギターの力学 新訂 クラシックギター編 その２  素晴らしきかな　ガット弦 Domingo Esteso （1925年作）　を 再現してみました イントネーション： 「楽器の個々のピッチの正確さ」			究極の音律を提供する 　 This is the Patented　　 (特許第4383272) for your Classic Guitar #1,#2,#3 ガット弦
ギター弦が、ガット しかなかった時、　ギター音楽は今よりずつと綺麗だったと思います。 それは、音色だけでなく、音の狂いが、驚異的に少なかった・・・であろう、と言うことが分かりました。

ナイロン弦を使用するクラシックギター・・・セゴビヤ　が使い始めて、ポピュラーになったと言われています。

ナイロン・・・1930年代に発明されたものですから、まだ、６０年ちょっとしか歴史はありません。　しかし、ギターは、何百年もの歴史があります。

その間、ずっと使われていた弦は、子羊の腸から作られる　ガット弦で、殆どの弦楽器は、この弦を使っていました。

　今では、バイオリンやチェロなどの弓奏楽器用としては、まだポピュラーに使われていますが、ギター用の弦としては、殆ど使われなくなってしまい、入手も結構面倒です。
しかし、ガット弦の特性を調べて見ますと、当時のギターは　音の狂いが、驚異的に少なかった・・・であろう・・・と言うことが分かりました。

　今では、ギター弦の著名なメーカーが、ナイロン弦を、如何にガット弦の特性に近づけるかを研究し、新しい弦を色々と製品化しています。　それらについては、また別な機会にご紹介するとして、ここでは、ガット弦をギターに張ると、どういうことになるか・・・をご紹介致します。

ガット弦を張る前の、クラシックギター

下左のギターの写真は、 Minehara Super Tune System  適応済みです。

弦長：　650mm

サドル 調整　は　第３弦のみ

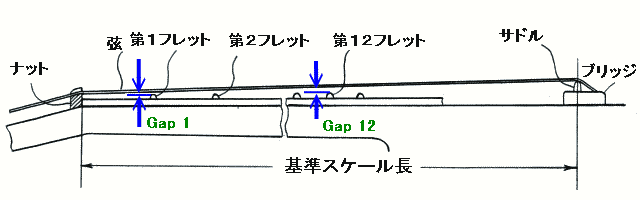
Minehara Super Tune System  適応前 （注）データのないフレットは、測定を省略してあります。

フレット位置と弦

ギターのフレット位置の計算方法は、Rule of Eighteen  (１８　のルール)　と呼ばれる方法で計算される、と言うことは、こちらでご説明しました。

---

このギターは　基準スケール長 650mm で設計されていますので、弦長 (ナットからサドルまで)　は、ナットから第１２フレットまでの寸法の２倍の、　650mm 　より、僅かに長く設定されています。

このギターの場合、サドルの位置は、下記のような値に設定されています。

Fret #	基準スケール長 650mm 、 ナットからフレット位置までの寸法 (mm) 平均律　の計算値	第6弦 E	第5弦 A	第4弦 D	第3弦 G	第2弦 B	第1弦 E
0	0	サドルは、第６弦側の弦長が長くなるように、僅かに傾いています。
1	36.480
2	70.915
3	103.419
4	134.094
5	163.050
6	190.379
7	216.178
8	240.525
9	263.507
10	285.200
11	305.675
12	325.000
	ナットからサドルまでの弦長	651.5	651.3	651.2	652.0	651.0	650.9

第3弦 　G　のみ、弦長が特別に長くなるように、サドルの部分で弦長を補正して、正確なピッチに近づける工夫がなされています。

---

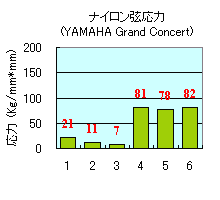
ナイロン弦　は、下記の弦が使われていました。

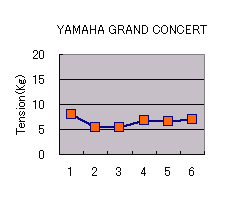
YAMAHA Grand Concert String
	String	ゲージ (in)	芯線	弦張力	弦の応力
	#1	.028	.028 in (モノフィラメント)
	#2	.032	.032 in (モノフィラメント)
	#3	.040	.040 in (モノフィラメント)
	#4	.028	20μm ×270本 (フロス)
	#5	.035	20μm ×270本 (フロス)
	#6	.043	20μm ×270本 (フロス)

（注）　上に示したデータは、メーカーが公表しているものでは有りません。工房ミネハラ　が参考値として、 計算、あるいは実測した値です。　弦張力・応力　などは、計算によって求めてあります。

---

クラシックギターのナイロン弦は、２種類の弦が使われています。　通常、第１、２、３弦　に使われている、モノフィラメント　と言って、１本のナイロン弦 です。

クラシックギター　ナイロン第６弦

一方、上の写真は、クラシックギターの第６弦の端の部分をほどいた物です。　極　細い、ナイロンフロス　floss (綿毛)　と言う繊維 (フィラメント) を撚って、その上に、銀メッキした銅線を巻いた弦です。

ナイロン弦のクラシックギター　では、通常、第４、５、６弦　に、このような構造の弦が使われています。

皆さん・・・、弦１本に、何本の繊維 (フィラメント) が使われているか・・・、数えたことはありますか？？？　工房ミネハラ　は、暇に任せて、数えて見ました。　その結果は、 上の表のような本数した。

また、フロスの直径　20ミクロン　(１ミクロンは、1/1000 mm) は、極細繊維のため、多少バラつきが測定されましたが、平均値としてこの値を使用しました。フロスの本数は、四捨五入した値です。

ご参考までに：　私の髪の毛の太さは、７０ミクロンでした。　フロスの直径　20ミクロン　は、髪の毛の１／４　の太さです。

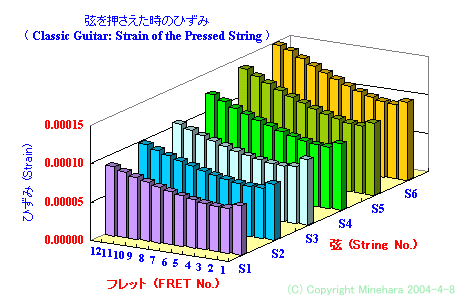
弦が押さえつけられた時に伸ばされる量・・・ひずみ　に対する感度は、モノフィラメント　の弦より小さく、音程の狂いが少ない・・・と言うことを ご説明しました。

---

クラシックギターの音程の狂いを考えるとき、

音程の狂い　の　最大の問題は、 ０．８−１ｍｍ程度の太い、モノフィラメント　の弦に有ります。 弦張力・応力　は、比較的、小さいのに・・・何故・・・？？？ 実は、弦張力・応力　が小さい弦の方が、 弦が押さえつけられた時に伸ばされる量・・・ひずみ　に対する　音程の狂い　は大きいのです。

と言う、問題点もご説明しまた。

復習は以上にして、上でご紹介したクラシックギターに、ガット弦　を張ってみました。

クラシックギター　の、ガット弦　とは。

（英）Northern Renaissance Instruments 社　のホームページによると、歴史的に下表のような弦が使われていた・・・とあります。

	弦の種類	２０世紀初めの Light-Medium ゲージ (mm)	後期１９世紀の Light-Medium ゲージ (mm)
1 st e	Twist Gut String	0.57-0.61	0.61-0.64
2 nd b	Twist Gut String	0.68-0.72	0.76-0.81
3 rd g	Twist Gut String	0.86-0.91	0.96-1.02
4 th d	Wound on Silk	1.14-1.21	1.28-1.36
5 th A	Wound on Silk	1.53-1.62	1.71-1.82
6 th E	Wound on Silk	2.04-2.16	2.29-2.42

年代とともに、良い音を響かせるために、細いゲージの弦が使われるようになってきたようです。

 Wound on Silk 　弦は、上でご紹介した、現在の　ナイロン弦セットの 第４、５、６弦　の芯線部が、 絹糸  で出来たもので、弦の特性は、現在の　ナイロン弦セットの 第４、５、６弦　に殆ど似たものです。

一方、 Twist Gut String 　弦は、子羊の腸の繊維のみを撚り合せて作った弦です。

---

では、そのガット弦は、どのように作られるのか・・・を説明いたします。

乾燥した山地の牧草地で育った羊の体内から取り出された腸は、中の内容物や脂肪分をナイフでしごいて取り出し、綺麗にされる。

１２−１５時間ほど冷水に浸し、さらに温湯に浸して繊維の分離を助けながら、さらに腸をしごいて繊維膜を取り出す。 アンモニヤ溶液の中に３−４時間浸した後、更にしごいて余分な膜を取り除く。この作業を数回繰り返す。

この後、２−３日かけて中和させる。 腸を細い糸状に裂く。

これを捻りながらガットを束ねて必要な太さにする。 腸に含まれるにニカワ質で自然に粘着する。

 Twist Gut String 　ガット弦は、腸の繊維のみで作られていることがわかりました。　（通常、表面処理はされています）

---

(仏)SAVAREZ 社　BRH 84 (0.84mm)

この写真は、実際の、 Twist Gut String 　ガット弦の先を、ハンマーで軽く叩いて、解してみた物です。　なーるほど・・・。

上の、ナイロンフロス　floss (綿毛)　と全く良く似ています。　これが、大切なポイントです。

---

では、実際に、ギターに張ってみましょう。

クラシックギター　に、ガット弦　を張る。

写真の、黒い印は、弦の伸び（ひずみ）を測定するために付けたマークです。

今回の実験では、下の　第４、５、６弦　は、ナイロンフロス 弦　のままとして、第１，２，３弦　のみ、 Twist Gut String 　ガット弦を張りました。　弦の張力、応力は、計算により求めました。

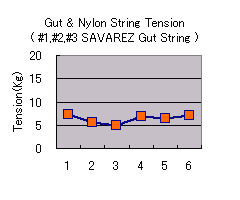
SAVAREZ Gut String (#1,#2,#3) & YAMAHA Grand Concert String (#4,#5,#6)
String	ゲージ	芯線	弦張力	弦の応力
#1	.63 mm	.63 mm (ツイストガット)
#2	.74 mm	.74 mm (ツイストガット)
#3	.84 mm	.84 mm (ツイストガット)
#4	.028 in	20μm ×270本 (フロス)
#5	.035 in	20μm ×270本 (フロス)
#6	.043 in	20μm ×270本 (フロス)

弦の張力、応力は、計算により求めました。　第４、５、６弦　は、上の表の数値と同じです。　 Twist Gut String 　ガット弦の応力は、張力を弦の断面積で割った物ですが、正確にはニカワ質の部分には力が働きませんので、繊維部の断面積は弦の直径から計算で求められる値より小さいと考えられます。　従って、 Twist Gut String 　ガット弦の応力は、上の計算値よりもっと大きいと推定されます。

---

 Twist Gut String 　ガット弦を張った後、弦がどの位伸びるか・・・これを、ひずみ　と言いますが、・・・測定して見ました。　ご覧下さい。

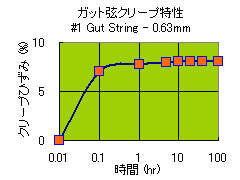
Twist Gut String 　0.63 mm

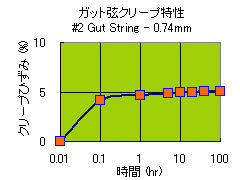
Twist Gut String 　0.74 mm

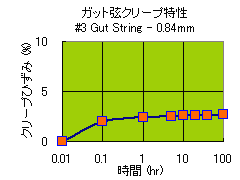
Twist Gut String 　0.84 mm

ひずみ　が、時間とともにどんどん大きくなってます、　このような現象を、クリープひずみ　と言いますが、要は、どんどん伸びている・・・と考えて下さい。

便宜上、張る前の長さを、0.01 hr としましたが、0.1 hr すなわち、６分後には、相当伸びて、１ｈｒ　後には、殆ど伸び切ったように見えませんか。
正確には、２４ｈｒ（１昼夜）位で、カーブはほぼ水平になりました。　 Twist Gut String 　0.63 mm　の場合、クリープひずみ　の値は、約 ８％ですので、弦長 650mm の場合、約　５ｃｍ　位い伸びたことになります。 また、７２ｈｒ（３昼夜）　後に、弦を全部緩めて見ましたところ、約　３％　の永久変形（伸びが元に戻らない量）が観測されました。

---

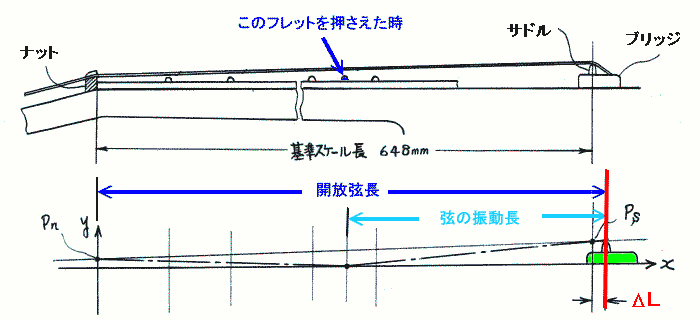
このギターの力学　でテーマとしている、弦をフレットに押さえた時の、音程の狂い を計算で求める方法は、アコースティックギターを例として、こちらで詳しくご紹介しています。　が、重要なポイントは、引っ張られた弦が、どのような状態なのか・・・と言うことです。

通常のチューニングで調弦したときに対して、それより　半音低い　或いは、半音高い音　に弦の張力を変えると、弦はどれだけ伸びる量が変わるか・・・と言う量を　半音ひずみ　Δεs　と 定義しました。

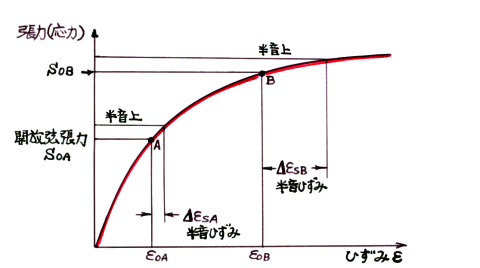
下の図は、弦の半音ひずみ　Δεs　を、模式的に示したものです。

Ａ点　では、弦の張力（応力）は小さいところで使用しています。　このような状態では、半音ひずみ　ΔεsA　が小さな量でも、弦の音程は半音上がります。

一方、Ｂ点　では、弦の張力（応力）は大きなところで使用しています。　このような状態では、半音ひずみ　ΔεsB　は相当大きな量にしないと、弦の音程は半音上がりません。

Ｂ点　は、糸巻きを　何回も・・・何回も・・・グルグル巻いたような状態です。

---

ナイロンフロス　floss (綿毛)　の性質については、こちらでご説明しましたが、 Twist Gut String 　ガット弦も、それと全く同じような特性を持つ弦で、Ｂ点　のような状態で使われる弦・・・と言うことが分かりました。

普通のナイロン弦セットに入っている　モノフィラメント　の、第１，２，３　弦は、応力　10-20 Kg/mm*mm 程度で使われていますので、Ａ点　のような状態で使われています。

直感的に分かることは、伸び切った状態で使われている弦　これは、あとちょっと伸びたからと言って、弦の張力が、それ程大きく変わる・・・とは、思われません。

　

---

このギターの力学　でテーマとしている、弦をフレットに押さえた時の、音程の狂い を計算で使用する、 Ｋｅ 　 の値求めてみましょう。

 Ｋｅ 　 の値は、通常のチューニングで調弦したときに対して、それより　半音低い　或いは、半音高い音　に弦の張力を変えると、弦はどれだけ伸びる量が変わるか・・・と言う量を　半音ひずみ　Δεs　から求めています。　こちらで詳しくご紹介しています。

 Ｋｅ 　= ( 1.0594631×1.0594631- 1 ) ÷ Δεs

　

YAMAHA Grand Concert String   の値、　Ｋｅ　の値は、下記のよう な値でした。

#	Note	弦の振動数  (Ｈｚ)	弦	弦のゲージ (inch)	弦の外径 (mm)	芯線	弦の張力  (Kg)	弦の応力  (Kg/sq-mm)	半音ひずみ　Δεs	Ｋｅ
1	E	329.6	モノフィラメント	.028	0.71	.028 in	7.9	21	0.0022	56
2	B	246.9	モノフィラメント	.032	0.81	.032 in	5.4	11	0.0019	64
3	G	196.0	モノフィラメント	.040	1.02	.040 in	5.3	7	0.0012	102
4	D	146.8	ナイロンフロス	.028	0.71	20μm ×270本	6.9	81	0.0026	47
5	A	110.0	ナイロンフロス	.035	0.89	20μm ×270本	6.5	78	0.0026	47
6	E	82.4	ナイロンフロス	.043	1.09	20μm ×270本	7.0	82	0.0026	47

（注）　モノフィラメント 弦は、引っ張られた状態で、3-4% 程度、直径が細くなります。　弦の応力は、細くなった線径で計算しています。

---

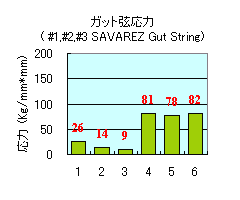
これに対して、今回、実験に使用した、SAVAREZ Gut String (#1,#2,#3 に使用) は、下記のような値が観測されました。

SAVAREZ Gut String  を使用した場合の　 Ｋｅ 　の値

#	Note	弦の振動数  (Ｈｚ)	弦	弦のゲージ (mm)	弦の外径 (mm)	弦の張力  (Kg)	弦の応力  (Kg/sq-mm)	半音ひずみ　Δεs	Ｋｅ
1	E	329.6	Twist Gut String	.63	0.63	7.3	26	0.0041	30
2	B	246.9	Twist Gut String	.74	0.74	5.7	14	0.0027	45
3	G	196.0	Twist Gut String	.84	0.84	4.9	9	0.0017	72

（注）　 Twist Gut String も、引っ張られた状態で、2-5% 程度、直径が細くなります。　弦の応力は、細くなった線径で計算しています。

---

これを比較して見ると、 Twist Gut String 　 Ｋｅ 　の値は、第３弦を除けば、通常の　ナイロン弦セットより小さく、従って、音程の狂い　も少ない弦・・・と言うことが分かりました。

第３弦に関しても、モノフィラメント 弦　に比べて、３０％程度小さく、ガット弦の使用は、音程の狂い　を小さくする効果は大きいと考えられます。

では、実際のギターの、音程の狂い　の状態を、シミュレーション計算と、実測値を見てみましょう。

ガット弦を使うと、確かに　音程の狂い　は小さかった･･･

計算の過程は、こちらと同じ・・・ですので、結果のみご紹介します。

弦高　こちらと同じです。

　

フレットを押さえた時の、弦の　Δε　（ひずみ）　の値 こちらと同じです。

---

　

弦をフレットに押さえた時、どれくらい音が高くなってしまうか・・・実際の音程の狂い を計算結果

計算方法の詳細は、各章で詳しく解説していますので、ここでは、その結果のみ示します。

	比較のため、　ナイロン弦　クラシックギター　も一緒に載せました。
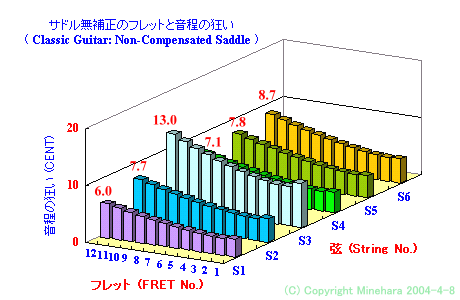
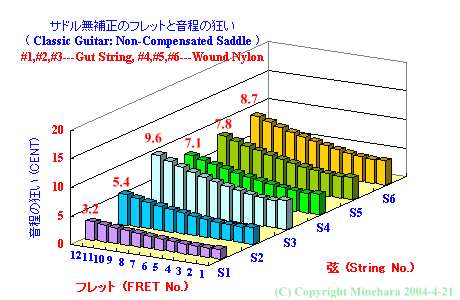
ガット弦使用　クラシックギター	ナイロン弦　クラシックギター
サドル無補正状態のフレットと音程の狂い	サドル無補正状態のフレットと音程の狂い

第１、２、３弦　は、　ガット弦使用　クラシックギター　　の方が小さくなっています。　第４、５、６弦　は、ナイロンフロス 弦　を使っていますので、両者の値は同じです。　

---

サドルポジションの補正が完全に行われた場合の、音程の狂い の計算結果

　

ガット弦使用　クラシックギター	ナイロン弦　クラシックギター
理想的サドル補正後のフレットと音程の狂い　（計算値）	理想的サドル補正後のフレットと音程の狂い　（計算値）

　

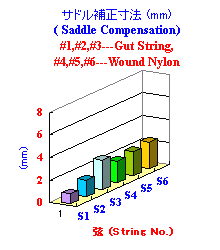
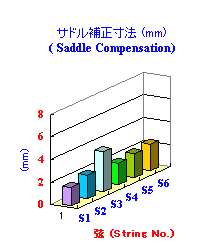
理想的サドル位置の補正量 　ΔＬ (mm)　は、下記の値となります。

#	Note	弦の振動数  単位：Ｈｚ	理想的サドル位置の補正量計算値 　ΔＬ (mm)
1	E	329.6	0.9
2	B	246.9	1.5
3	G	196.0	2.6
4	D	146.8	1.9
5	A	110.0	2.1
6	E	82.4	2.4

　

理想的サドル位置の補正量の試算結果

ガット弦使用　クラシックギター	ナイロン弦　クラシックギター

理想的サドル位置の補正量も、　ガット弦使用　クラシックギター　　の方が小さくなっています。　これは、下の写真のような、一本のサドルで良い事を物語っています。

上の写真の実際のサドルの場合、 第１弦の弦長を、基準スケール長　 の、650mm　より、約1mm。　第６弦の弦長を、基準スケール長　 の、650mm　より、約1.5mm 長くする位置に設定されていました。

しかし、サドルの厚みは、2.4mm しかなく、　全ての弦に対して、上の、理想的サドル位置の補正量　ΔＬ (mm)　の値にサドルの位置を設定することが不可能なのです。
理想的な値より、１ｍｍ程度、補正量が不足する弦があり、音程の狂い　は、残ってしまっています。

　

---

　

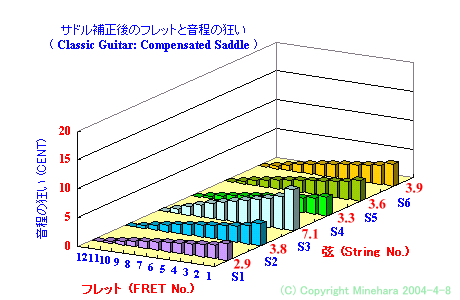
サドル補正後の　音程の狂い　は、どの程度あるのでしょうか・・・　ここで は、実測結果を示します。

　

ガット弦使用　クラシックギター	ナイロン弦　クラシックギター
（実測値）	（実測値）

（注）データのないフレットは、測定を省略してあります。

　ガット弦使用　クラシックギター　　の第１、２、３弦　は、サドル補正量が小さな値で良かったため、　実際のサドル補正量　で随分と音程の狂いは小さくなりました。

しかしながら （１）　理想的サドル補正　が出来れば、第１２フレット　の音程の狂いは、全く無くなるはず・・・。 （２）　でも、実際は、理想的サドル補正　が出来ていないため、第１２フレット側　で、音程の狂い　は、依然として残ってしまっている。 （３）　もし、理想的サドル補正　が出来たとしても、ローポジション の　音程の狂い　はまだ完全にはなくならない。

　

ポイント 弦高調整　や　サドル調整　（コンペンセイテッドサドル） がよく出来ていれば、ガット弦を使ったクラシックギターは、相当に　正確なイントネーション 　が確保出来ていた。 と言えるのではないでしようか。 これが、 ギター弦が、ガット しかなかった時、　ギター音楽は今よりずつと綺麗だった・・・と 考えられる所以です。 　　　　(注)　イントネーション　：　「楽器の個々のピッチの正確さ」

残った課題を　解決するのが

Patented　　 (特許第4383272)

です。

これを、Domingo Esteso （1925年作）　や　Jose Ramirez �V（1965年作）　達は、 更に工夫を行っていたと思われます。

---

クラシックギターの不思議　では、Domingo Esteso （1925年作）　や　Jose Ramirez �V（1965年作）　が、

何れのギターも、第１フレット　の寸法 を、平均律で計算 される値より、短く設定　していることを説明しました。

The distance between the nut and the first fret are 1% to 1.7% shorter than the "Rule of Eighteen" standard.

この辺が、名工たちが作ったギターの　音律を正しくする秘密　では無いか？？・・・といいましたが、

それは一理あるようです。

---

第１フレット　の寸法が、平均律で計算 される値より、短く設定　されている・・・と言うのは、どういうことでしょうか。

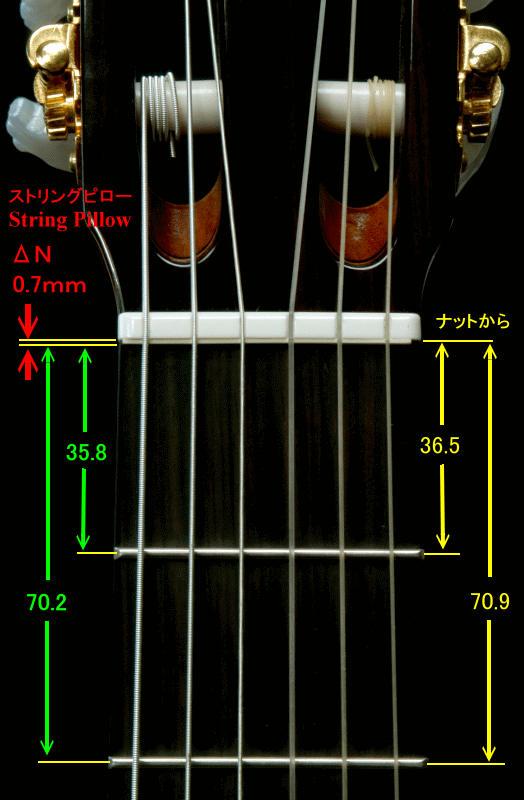
下の写真をご覧下さい。　これは、 Minehara Super Tune System  で使用する、 従来のナットの直ぐそばに、第１フレットまでの寸法を短縮させる、ストリングピロー　と言うパーツです。

Domingo Esteso （1925年作）　を　再現してみました

８０年以上前のギターを、そのまま再現させることは、ちょっと難しかったため、基準スケール長 650mm で作られているギターを、 Minehara Super Tune System  で再現しました。

このページの冒頭に示したギターの表に記入されている、基準スケール長 650mm 、ナットからフレット位置までの寸法 (mm)　平均律　の計算値　をご覧になって下さい。

下記のような寸法です。

Fret #	基準スケール長 650mm 、ナットからフレット位置までの寸法 (mm) 平均律　の計算値
0	0
1	36.480
2	70.915
3	103.419
4	134.094
5	163.050
6	190.379
7	216.178
8	240.525
9	263.507
10	285.200
11	305.675
12	325.000

　

今回、ガット弦を張った、実験に使用しているギターは、基準スケール長 650mm で作られていますので、第１フレットは、 36.5 mm , 第２フレットは　 70.9 mm  ・・・に有ります。

このギターに、ΔＮ= 0.7 mm の　ストリングピロー　をセットしました。

その結果、第１フレットは、 35.8 mm , 第２フレットは　 70.2 mm  ・・・に変わり、

下の写真のようなギターになります。

　

ここで、もう一度、　Domingo Esteso （1925年作）　をご覧下さい。

　

詳細は　 クラシックギターの不思議　で、ご紹介しています。

　

このギターの第１フレットは、 35.8 mm , 第２フレットは　 70.2 mm  ・・・、上の写真のギターと同じ寸法だと思います。

この状態で、音程の狂い　を実際に測定してみました。

このデータをご覧下さい ストリングピロー使用後　の　音程の狂い　は、こんなに小さくなります。

ガット弦使用　クラシックギター	ガット弦使用　クラシックギター
ストリングピロー使用後　の　音程の狂い　（実測値） ・・・これなら、全く音程の狂いは気にならないと思います。 　この状態は、Domingo Esteso (1925年作) と、全く同じです	ストリングピローを使用しない状態の　音程の狂い　（実測値） （注）データのないフレットは、測定を省略してあります。

今回、この実験を行うまでは、

クラシックギターの不思議　では、Domingo Esteso （1925年作）　や　Jose Ramirez �V（1965年作）　が、

何れのギターも、第１フレット　の寸法 を、平均律で計算 される値より、短く設定　していることを説明しました。

The distance between the nut and the first fret are 1% to 1.7% shorter than the "Rule of Eighteen" standard.

この辺が、名工たちが作ったギターの　音律を正しくする秘密　では無いか？？・・・といいましたが、

それは一理あるようです。

と、多少、半信半疑のところも無くは無かったのですが、この実験を行って、　この仮説は正しかった　・・・と言うことの確信がもてました。

現在のギターでは、ガット弦は使わない・・・ 　そこで、ナイロン弦　クラシックギター　でも、

弦の性質　に合わせた、ストリングピロー位置  ΔＮ (mm)　と　サドル位置の補正量　ΔＬ (mm)　 の設定を行えば、

音程の狂い の全く無いギターを手にできる・・・これが、 Minehara Super Tune System 　です。

　

（例）　YAMAHA Grand Concert String   使用時の　ストリングピロー位置  ΔＮ (mm)　と　サドル位置の補正量　ΔＬ (mm)　の関係

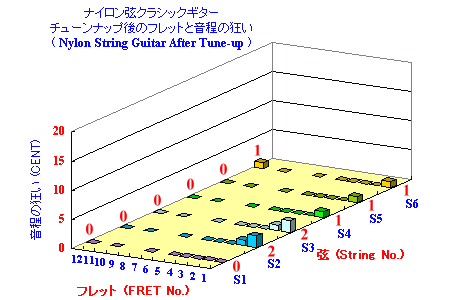
このデータをご覧下さい 　ナイロン弦　クラシックギター　でも、 ストリングピロー使用後　の　音程の狂い　は、こんなに小さくなります。

Minehara Super Tune System 　使用時
ストリングピロー使用後　の　音程の狂い　　（計算値） ・・・これなら、全く音程の狂いは気にならないと思います。	ストリングピロー使用後　の　実際のギターの　音程の狂い　（実測値） （注）データのないフレットは、測定を省略してあります。
弦の性質に合わせて補正された　ストリングピロー	弦の性質に合わせて補正されたサドル

これは、上の、　　ガット弦使用　クラシックギター　　に、　ΔＮ= 0.7 mm の　ストリングピロー　を使ったものと、全く同じように、音程の狂い　の 無いギターとなっています。

Minehara Super Tune System  使用前

このギターを、
　

 Minehara Super Tune System 　使用時

に変身させる・・・

　ミネハラ スーパーチューンシステム

フロントページ

弦楽器の力学　のページで掲載しているデータの無断転載 ・公開等はお断りします。

---

工房ミネハラ
Mineo Harada

Updated:2009/10/6

First Updated:2004/4/22